Inhaltsverzeichnis
01. Was versteht man unter dem Begriff „Anwendungs-Software“?
Als Anwendungs-Software bezeichnet man Programme, die von einem Anwender (Benutzer) zur Lösung seiner speziellen Aufgaben mittels eines Computers eingesetzt werden. Will ein Benutzer einen Brief schreiben, so steht ihm dafür als Anwendungs-Software ein Textverarbeitungsprogramm zur Verfügung. Sollen Adressdaten verwaltet werden, so kann ein Datenbankprogramm als Anwendungs-Software gewählt werden.
02. Wozu dient Standard-Software?
Unter Standard-Software versteht man Programme, die einen festen Leistungsumfang haben und die aufgrund ihrer allgemeinen Ausrichtung möglichst viele Anwender ansprechen sollen. Daher handelt es sich bei den Anwendungen der Standard-Software sehr häufig um Standard-Anwendungen wie z. B. Textverarbeitung, Tabellenkalkulation, Datenbankverwaltung etc. Da Standard-Software in hohen Stückzahlen produziert und verkauft werden kann, sind die Preise entsprechend gering.
03. Wo findet Individual-Software Anwendung?
Wie der Name sagt, handelt es sich hierbei um speziell auf den einzelnen Anwender zugeschnittene Software. Die Software wird meist nach den Wünschen des Anwenders entwickelt, sodass dieser auch den genauen Leistungsumfang vorgibt. In der Regel kommt eine solche Individual-Software auch nur bei einem Anwender zum Einsatz. Beispiel für den Einsatz von Individual-Software ist der Bereich der Betriebsdatenerfassung. Da eine Individual-Software für einen Anwender entwickelt wird, sind die Kosten entsprechend hoch.
04. Was ist bei der Interpretation von Diagrammen zu beachten?
Hinweis:
Wir beschränken uns an dieser Stelle auf einige Hinweise zur Interpretation von Diagrammen.
Bei Diagrammen mit ungenauen Bezeichnungen und Angaben kann es zu Fehlinterpretationen kommen, z. B.:
Titel: Was soll im Diagramm dargestellt werden/sein?
Maßstab:
Welcher Maßstab wurde gewählt?
auf der Ordinate (= senkrechte y-Achse)?
auf der Abszisse (= waagerechte x-Achse)?
natürliche Zahlen, Dezimalzahlen, Prozentzahlen, Logarithmen, Indexzahlen, Schrittfolge im Maßstab.
Sind die Proportionen der Achsen zueinander so gewählt, dass keine Verzerrung entsteht?
Sind die Maßeinheiten vorhanden, richtig gewählt und einheitlich (z. B. kg, t, €, T€ usw.)?
Fläche: Existieren Gitterlinien, sodass Zahlenwerte aus dem Diagramm exakt ablesbar sind?
Diagrammart:
Entspricht die Art des Diagramms dem darzustellenden Problem, z. B.:
Anteile → Kreisdiagramm, Struktogramm
Zeitreihe → Liniendiagramm
Häufigkeit → Säulendiagramm, Stabliniendiagramm.
Diagramme müssen durch die Art ihrer Darstellung die beabsichtigte Aussage dem Betrachter deutlich mitteilen. Mitunter sind Diagramme mit zu vielen Effekten überfrachtet, sodass der Aussagewert leidet (z. B. Schattierung, Rasterung, Schriftarten, 3-D-Darstellung).
Kreisdiagramme sind z. T. sehr effektvoll. Für den Betrachter lassen sich jedoch die Proportionen der Kreissegmente nur schwer abschätzen.
Der Betrachter sollte den Hintergrund des Datenmaterials kennen, z. B.:
Wann wurde das Datenmaterial erfasst?
Wie erfolgte die Erfassung (manuelle Messung, Sensoren u. Ä.)
Sind Urlistendaten dargestellt oder wurde das Datenmaterial bereits verdichtet (z. B. durch die Bildung von Merkmalsklassen)?
Welcher Prozess liegt zu Grunde?
Beispiel
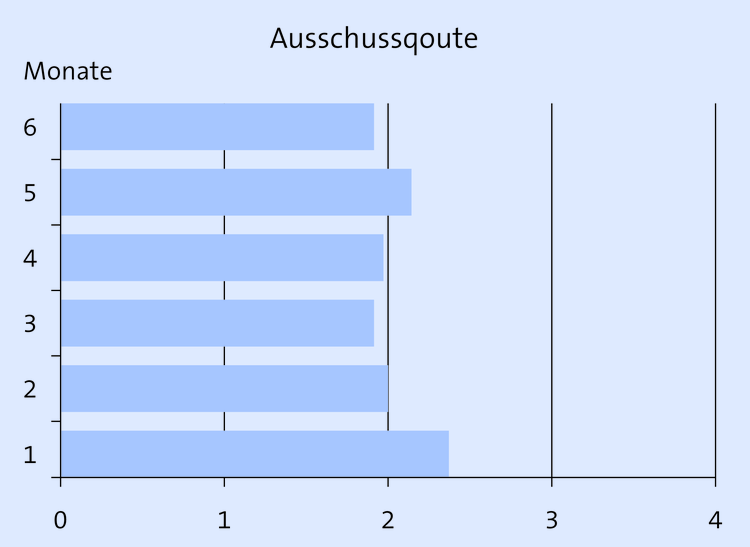
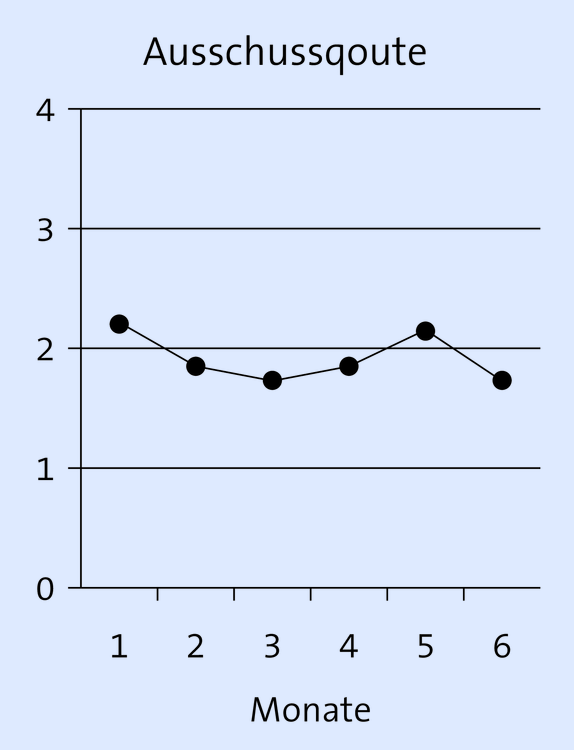
Die nachfolgend dargestellten Diagramme (Abb. 1 bis 3) zeigen denselben Sachverhalt und basieren auf demselben Datengerüst. Die Abbildungen sind zum Teil mit Fehlern behaftet, sodass der Betrachter zu Fehlinterpretationen kommen kann:
In Abbildung 2, unten, fehlt die Maßeinheit an der Abszisse, bei Abb. 1 und 3 fehlt die Maßeinheit an der Ordinate (vermutlich Prozent?); außerdem ist der Titel nicht aussagefähig (Ausschussquote: Wann? Bei welchem Prozess?).
Bei Abbildung 1 ist der Maßstab der Abszisse zu groß gewählt, sodass der Eindruck entstehen kann, dass kaum Schwankungen des Merkmals zu verzeichnen sind. Ein umgekehrtes Bild ergibt sich beim 3. Diagramm. Hier wurde der Maßstab der Abszisse zu klein gewählt im Verhältnis zur Ordinate.
Weiterhin wäre zu klären, welche Diagrammart den Sachverhalt deutlicher ausweist? Abbildung 2 hat z. B. den Vorteil, dass der Betrachter aufgrund der waagerechten Darstellung der Säulen und der senkrechten Gitterlinien die einzelnen Messwerte exakt aus dem Diagramm ablesen kann.
Für alle drei Diagramme stellt sich die Frage, warum der Ersteller der Abbildungen darauf verzichtet hat, das Datengerüst in Form einer Tabelle mit anzugeben?
Weitere interessante Inhalte zum Thema
-
Kapitel 8 - Mind Mapping Software
Vielleicht ist für Sie auch das Thema Kapitel 8 - Mind Mapping Software (Mind Mapping Onlinekurs) aus unserem Online-Kurs Mind Mapping interessant.