Inhaltsverzeichnis
- 01. Welche Kalkulationsverfahren muss der Industriemeister anwenden können?
- 02. Wie ist das Verfahren bei der einstufigen Divisionskalkulation?
- 03. Wie ist das Verfahren bei der mehrstufigen Divisionskalkulation?
- 04. Wie ist das Verfahren bei der Divisionskalkulation mit Äquivalenzziffern?
- 05. Wie ist das Verfahren bei der summarischen Zuschlagskalkulation?
- 06. Wie ist das Verfahren bei der differenzierten Zuschlagskalkulation?
- 07. Wie werden Maschinenstundensätze (im Rahmen der differenzierten Zuschlagskalkulation) berechnet?
- 08. Wie wird der Minutensatz bei der Kalkulation mit Maschinenstundensätzen ermittelt?
01. Welche Kalkulationsverfahren muss der Industriemeister anwenden können?
Je nach Produktionsverfahren werden verschiedene Kalkulationsverfahren angewendet. Die Grundregel lautet:
Das Produktionsverfahren bestimmt das Kalkulationsverfahren.
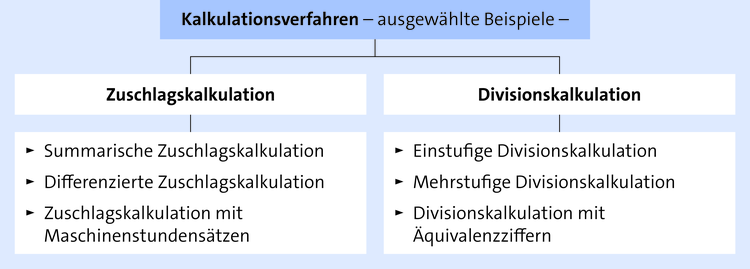
Der Rahmenstoffplan nennt folgende, ausgewählte Verfahren der Kalkulation:
02. Wie ist das Verfahren bei der einstufigen Divisionskalkulation?
Voraussetzungen:
Massenfertigung; Einproduktunternehmen (z. B. Energieerzeuger: Stadtwerke, Wasserwerke)
einstufige Fertigung
keine Kostenstellen
keine Aufteilung in Einzel- und Gemeinkosten
produzierte Menge = abgesetzte Menge; xP = xA
Berechnung:
Die Stückkosten (k) ergeben sich aus der Division der Gesamtkosten (K) durch die in der Abrechnungsperiode produzierte und abgesetzte Menge (x).
$$Stückkosten = \frac{Gesamtkosten}{Ausbringungsmenge}$$
$$k = \frac{K}{x}\; €/Stk.$$
Beispiel
Ein Einproduktunternehmen produziert und verkauft im Monat Januar 1.200 Stk. bei 360.000 € Gesamtkosten. Die Stückkosten betragen:
$$k = \frac{K}{x}\; €/Stk.$$
$$= \frac{360.000 €}{1.200\; Stk.} = 300 €/Stk.$$
03. Wie ist das Verfahren bei der mehrstufigen Divisionskalkulation?
Voraussetzungen:
Massenfertigung; Einproduktunternehmen
zwei oder mehrstufige Fertigung
produzierte Menge ≠ abgesetzte Menge; xP ≠ xA
Aufteilung der Gesamtkosten (K) in Herstellkosten (KH) sowie Vertriebskosten (KVertr.) und Verwaltungskosten (KVerw.)
die Herstellkosten werden auf die produzierte Menge (xP) bezogen, die Vertriebs- und Verwaltungskosten auf die abgesetzte Menge (xA).
Berechnung:
Bei einer zweistufigen Fertigung ergibt sich folgende Berechnung:
$$Stückkosten = \frac{Herstellkosten}{produzierte\; Menge} + \frac{Vertriebs-\; und\; Verwaltungskosten}{abgesetzte\; Menge}$$
$$Stückkosten = \frac{K_{H}}{x_{P}} + \frac{K_{Vertr.} + K_{Verw.}}{x_{A}}$$
Beispiel
Beispiel 1:
Ein Betrieb produziert im Monat Januar 1.200 Stk., von denen 1.000 verkauft werden. Die Herstellkosten betragen 240.000 €, die Vertriebs- und Verwaltungskosten 120.000 €. Die Stückkosten sind:
$$Stückkosten = \frac{240.000 €}{1.200 Stk.} + \frac{120.000 €}{1.000 Stk.}/ = 200 €/Stk. + 120 €/Stk = 320 €/Stk.$$
Beispiel 2:
Die Herstellkosten betrugen im Juni d. J. 400.000 €, die Vertriebs- und Verwaltungskosten 100.000 €. Die produzierte und abgesetzte Menge war 50.000 €. Im Oktober d. J. trat eine Absatzschwäche auf, sodass – unter sonst gleichen Bedingungen – 30 % der Fertigung auf Lager genommen werden musste. Zu ermitteln ist, um wie viel sich die Selbstkosten pro Einheit verändert haben.
Im Juni d. J. gilt:
$$k = \frac{K}{x}\; €/E$$
$$= \frac{500.000 €}{50.000\; E} = 10 €/E$$
Im Oktober d. J. gilt:
$$Stückkosten = \frac{K_{H}}{x_{P}} + \frac{K_{Vertr.} + K_{Verw.}}{x_{A}}$$
$$= \frac{400.000}{50.000} + \frac{100.000}{35.000} = 10,86 €/E$$
Die Produktion, die im Oktober d. J. zum Teil auf Lager genommen werden musste, erhöhte die Stückkosten um 8,6 % und verschlechterte die Liquidität.
Analog geht man bei einer n-stufigen Fertigung vor: Die Kosten je Fertigungsstufe werden auf die entsprechenden Stückzahlen bezogen:
$$Stückkosten = \frac{K_{H1}}{x_{P1}} + \frac{K_{H2}}{x_{P2}} + … + \frac{K_{Hn}}{x_{Pn}} + \frac{K_{Vertr.} + K_{Verw.}}{x_{A}}$$
04. Wie ist das Verfahren bei der Divisionskalkulation mit Äquivalenzziffern?
Voraussetzungen:
Sortenfertigung (gleichartige, aber nicht gleichwertige Produkte), z. B. Bier, Zigaretten, Ziegelei, Walzen von Blechen.
Die Stückkosten der einzelnen Sorten stehen langfristig in einem konstanten Verhältnis; man geht aus von einer Einheitssorte (Bezugsbasis), die die Äquivalenzziffer 1 erhält; alle anderen Sorten erhalten Äquivalenzziffern im Verhältnis zur Einheitssorte; sind z. B. die Stückkosten einer Sorte um 40 % höher als die der Einheitssorte, so erhält sie die Äquivalenzziffer 1,4 usw. Äquivalenzziffern werden durch Messungen, Beobachtungen, Beanspruchung der Kosten entsprechend den betrieblichen Bedingungen ermittelt.
produzierte Menge = abgesetzte Menge; xP = xA
Beispiel
In einer Ziegelei werden drei Sorten hergestellt. Die Gesamtkosten betragen in der Abrechnungsperiode 104.400 €. Die produzierten Mengen sind: 30.000, 15.000, 20.000 Stück. Das Verhältnis der Kosten beträgt 1 : 1,4 : 1,8.
| Sorte | Produzierte Menge (in Stk.) | Äquivalenzziffer | Recheneinheiten | Stückkosten (in €/Stk.) | Gesamtkosten (in €) |
| (1) | (2) | (3) | (4) | (5) | |
| I | 30.000 | 1,0 | 30.000 | 1,20 | 36.000 |
| II | 15.000 | 1,4 | 21.000 | 1,68 | 25.200 |
| III | 20.000 | 1,8 | 36.000 | 2,16 | 43.200 |
| Summe | 87.000 | 104.400 |
Rechenweg:
Ermittlung der Äquivalenzziffern bezogen auf die Einheitssorte.
Die Multiplikation der Menge je Sorte mit der Äquivalenzziffer ergibt die Recheneinheit je Sorte (= Umrechnung der Mengen auf die Einheitssorte).
Die Division der Gesamtkosten durch die Summe der Recheneinheiten (RE) ergibt die Stückkosten der Einheitssorte: 104.000 € : 87.000 RE = 1,20 €/Stk.
Die Multiplikation der Stückkosten der Einheitssorte mit der Äquivalenzziffer je Sorte ergibt die Stückkosten je Sorte: 1,20 • 1,4 = 1,68
Spalte [5] zeigt die anteiligen Gesamtkosten je Sorte (z. B.: 1,68 • 15.000 = 25.200). Die Summe muss den gesamten Produktionskosten entsprechen (rechnerische Probe der Verteilung).
05. Wie ist das Verfahren bei der summarischen Zuschlagskalkulation?
Voraussetzungen:
Die summarische Zuschlagskalkulation ist ein sehr einfaches Verfahren, das bei Serien- oder Einzelfertigung angewendet wird.
Die Gesamtkosten werden in Einzel- und Gemeinkosten getrennt. Dabei werden die Einzelkosten der Kostenartenrechnung entnommen und dem Kostenträger direkt zugeordnet.
Die Gemeinkosten werden als eine Summe („summarisch“; en bloc) erfasst und den Einzelkosten in einem Zuschlagssatz zugerechnet.
Es gibt nur eine Basis zur Berechnung des Zuschlagssatzes: entweder das Fertigungsmaterial oder die Fertigungslöhne oder die Summe (Fertigungsmaterial + Fertigungslöhne).
Beispiel
In dem nachfolgenden Fallbeispiel wird angenommen, dass Möbel in Einzelfertigung hergestellt werden. Die verwendeten Einzel- und Gemeinkosten wurden in der zurückliegenden Abrechnungsperiode ermittelt und sollen als Grundlage zur Feststellung des Gemeinkostenzuschlages dienen:
Fall A:
$$Gemeinkostenzuschlag = \frac{Gemeinkosten}{Fertigungsmaterial} \cdot 100$$
z. B.:
$$Gemeinkostenzuschlag = \frac{120.000 €}{340.000 €} \cdot 100 = 35,29 \%$$
Fall B:
$$Gemeinkostenzuschlag = \frac{Gemeinkosten}{Fertigungslöhne} \cdot 100$$
z. B.:
$$Gemeinkostenzuschlag = \frac{120.000 €}{260.000 €} \cdot 100 = 46,15 \%$$
Fall C:
$$Gemeinkostenzuschlag = \frac{Gemeinkosten}{Fertigungsmaterial + Fertigungslöhne} \cdot 100$$
z. B.:
$$Gemeinkostenzuschlag = \frac{120.000 €}{340.000 € + 260.000 €} \cdot 100 = 20,0 \%$$
Es ergeben sich also unterschiedliche Zuschlagssätze – je nach Wahl der Bezugsbasis:
| Fall | Zuschlagsbasis | Gemeinkostensatz |
| A | Fertigungsmaterial | 35,29 % |
| B | Fertigungslöhne | 46,15 % |
| C | Fertigungsmaterial + Fertigungslöhne | 20,00 % |
In der Praxis wird man die summarische Zuschlagskalkulation nur dann einsetzen, wenn relativ wenig Gemeinkosten anfallen; im vorliegenden Fall darf das unterstellt werden.
Als Basis für die Berechnung des Zuschlagssatzes wird man die Einzelkosten nehmen, bei denen der stärkste Zusammenhang zwischen Einzel- und Gemeinkosten gegeben ist (z. B. proportionaler Zusammenhang zwischen Fertigungsmaterial und Gemeinkosten).
Beispiel
Das Unternehmen hat einen Auftrag zur Anfertigung einer Schrankwand erhalten. An Fertigungsmaterial werden 3.400 € und an Fertigungslöhnen 2.200 € anfallen. Es sollen die Selbstkosten dieses Auftrages alternativ unter Verwendung der unterschiedlichen Zuschlagssätze (siehe oben) ermittelt werden (Kostenangaben in Euro).
Fall A:
Fall B:
Fall C:
Ergebnisbewertung:
Man erkennt an diesem Beispiel, dass die Selbstkosten bei Verwendung alternativer Zuschlagssätze ungefähr im Intervall [6.600; 6.800] streuen – ein Ergebnis, das durchaus befriedigend ist. Die Ursache für die verhältnismäßig geringe Streuung ist in den relativ geringen Gemeinkosten zu sehen.
Bei höheren Gemeinkosten (im Verhältnis zu den Einzelkosten) wäre die beschriebene Streuung größer und könnte zu der Überlegung führen, dass eine summarische Zuschlagskalkulation betriebswirtschaftlich nicht mehr zu empfehlen wäre, sondern ein Wechsel auf die differenzierte Zuschlagskalkulation vorgenommen werden muss.
06. Wie ist das Verfahren bei der differenzierten Zuschlagskalkulation?
Die differenzierte Zuschlagskalkulation (auch: selektive Zuschlagskalkulation) liefert i. d. R. genauere Ergebnisse als die summarische Zuschlagskalkulation (vgl. oben). Voraussetzung dafür ist eine Kostenstellenrechnung. Die Gemeinkosten werden nach Bereichen getrennt erfasst und die Zuschlagssätze differenziert ermittelt:
| Bereich | Gemeinkosten | Zuschlagsbasis |
| Materialbereich | Materialgemeinkosten | Materialeinzelkosten |
| Fertigungsbereich | Fertigungsgemeinkosten | Fertigungseinzelkosten |
| Verwaltungsbereich | Verwaltungsgemeinkosten | Herstellkosten des Umsatzes |
| Vertriebsbereich | Vertriebsgemeinkosten | Herstellkosten des Umsatzes |
Demzufolge werden die differenzierten Zuschlagssätze folgendermaßen ermittelt.
$$Materialgemeinkostenzuschlag = \frac{Materialgemeinkosten}{Materialeinzelkosten} \cdot 100$$
$$Fertigungsgemeinkostenzuschlag = \frac{Fertigungsgemeinkosten}{Fertigungseinzelkosten} \cdot 100$$
$$Verwaltungsgemeinkostenzuschlag = \frac{Verwaltungsgemeinkosten}{Herstellkosten\; des\; Umsatzes} \cdot 100$$
$$Vertriebsgemeinkostenzuschlag = \frac{Vertriebsgemeinkosten}{Herstellkosten\; des\; Umsatzes} \cdot 100$$
Für die differenzierte Zuschlagskalkulation wird bei dem Gesamtkostenverfahren folgendes Schema verwendet:
| Zeile | Kostenart | Abkürzung | Berechnung (Z = Zeile) | |
| 1 | Materialeinzelkosten | MEK | direkt | |
| 2 | + | Materialgemeinkosten | MGK | Z 1 • MGK-Zuschlag |
| 3 | = | Materialkosten | MK | Z 1 + Z 2 |
| 4 | Fertigungseinzelkosten | FEK | direkt | |
| 5 | + | Fertigungsgemeinkosten | FGK | Z 4 • FGK-Zuschlag |
| 6 | + | Sondereinzelkosten der Fertigung | SEKF | direkt |
| 7 | = | Fertigungskosten | FK | ∑ Z 4 bis 6 |
| 8 | = | Herstellkosten der Fertigung/Erzeugung | HKF | Z 3 + Z 7 |
| 9 | – | Bestandsmehrung, fertige/unfertige Erzeugnisse | BV+ | direkt |
| 10 | + | Bestandsminderung, fertige/unfertige Erzeugnisse | BV– | direkt |
| 11 | = | Herstellkosten des Umsatzes | HKU | ∑ Z 8 bis 10 |
| 12 | + | Verwaltungsgemeinkosten | VwGK | Z 11 • VwGK-Zuschlag |
| 13 | + | Vertriebsgemeinkosten | VtGK | Z 11 • VtGK-Zuschlag |
| 14 | + | Sondereinzelkosten des Vertriebs | SEKV | direkt |
| 15 | = | Selbstkosten des Umsatzes | SKU | ∑ Z 11 bis 14 |
Hinweise zur Berechnung:
Zeile 6:
Sondereinzelkosten der Fertigung fallen nicht bei jedem Auftrag an, z. B. Einzelkosten für eine spezielle Konstruktionszeichnung.
Zeile 9 – 10:
Bestandsmehrungen an fertigen/unfertigen Erzeugnissen haben zum Umsatz nicht beigetragen, sie sind zu subtrahieren (werden auf Lager genommen).
Bestandsminderungen an fertigen/unfertigen Erzeugnissen haben zum Umsatz beigetragen, sie sind zu addieren (werden vom Lager genommen und verkauft).
Zeile 14:
Sondereinzelkosten des Vertriebs (analog zu Zeile 6) fallen nicht generell an und werden dem Auftrag als Einzelkosten zugerechnet, z. B. Kosten für Spezialverpackung.
Beispiel
Wir kehren noch einmal zurück zu der Möbelfirma (vgl. Beispiel „summarische Zuschlagskalkulation“, 05.): Das Unternehmen will den vorliegenden Auftrag über die Schrankwand nun mithilfe der differenzierten Zuschlagskalkulation berechnen.
Folgende Daten liegen aus der zurückliegenden Abrechnungsperiode vor:
Fertigungsmaterial = 340.000 €
Fertigungslöhne = 260.000 €
Aus dem BAB ergaben sich folgende Gemeinkosten:
Materialgemeinkosten = 60.000 €
Fertigungsgemeinkosten = 30.000 €
Verwaltungsgemeinkosten = 10.000 €
Vertriebsgemeinkosten = 20.000 €
Für den Auftrag werden 3.400 € Fertigungsmaterial und 2.200 € Fertigungslöhne anfallen. Bestandsveränderungen sowie Sondereinzelkosten liegen nicht vor. Zu kalkulieren sind die Selbstkosten des Auftrags.
1. Schritt:
Ermittlung der Zuschlagssätze für Material und Lohn
$$MGK-Zuschlag = \frac{MGK}{MEK} \cdot 100$$
$$= \frac{60.000}{340.000} \cdot 100 = 17,65 \%$$
$$FGK-Zuschlag = \frac{FGK}{FEK} \cdot 100$$
$$= \frac{30.000}{260.000} \cdot 100 = 11,54 \%$$
2. Schritt:
Ermittlung der Herstellkosten des Umsatzes als Grundlage für die Berechnung des Verwaltungs- und des Vertriebsgemeinkostensatzes
| Materialeinzelkosten | 340.000,00 | |
| + | Materialgemeinkosten | 60.000,00 |
| + | Fertigungseinzelkosten | 260.000,00 |
| + | Fertigungsgemeinkosten | 30.000,00 |
| = | Herstellkosten des Umsatzes | 690.000,00 |
$$VwGK-Zuschlag = \frac{VwGK}{HKU} \cdot 100$$
$$= \frac{10.000}{690.000} \cdot 100 = 1,45 \%$$
$$VtGK-Zuschlag = \frac{VtGK}{HKU} \cdot 100$$
$$= \frac{20.000}{690.000} \cdot 100 = 2,90 \%$$
3. Schritt:
Kalkulation der Selbstkosten des Auftrages mithilfe des Schemas
| Materialeinzelkosten | 3.400,00 | ||
| + | Materialgemeinkosten | 17,65 % | 600,10 |
| = | Materialkosten | 4.000,10 | |
| Fertigungseinzelkosten | 2.200,00 | ||
| + | Fertigungsgemeinkosten | 11,54 % | 253,88 |
| = | Fertigungskosten | 2.453,88 | |
| Herstellkosten der Fertigung | 6.453,98 | ||
| = | Herstellkosten des Umsatzes | 6.453,98 | |
| + | Verwaltungsgemeinkosten | 1,45 % | 93,58 |
| + | Vertriebsgemeinkosten | 2,90 % | 187,17 |
| = | Selbstkosten (des Auftrags) | 6.734,73 |
Bewertung des Ergebnisses:
Man kann an diesem Beispiel erkennen, dass die Selbstkosten auf Basis der differenzierten Zuschlagskalkulation nur wenig von denen auf Basis der summarischen Zuschlagskalkulation abweichen. Die Ursache ist darin zu sehen, dass wir im vorliegenden Fall einen Kleinbetrieb mit nur sehr geringen Gemeinkosten haben. Es lässt sich zeigen, dass bei hohen Gemeinkosten die differenzierte Zuschlagskalkulation eindeutig zu besseren Ergebnissen als die summarische Zuschlagskalkulation führt.
07. Wie werden Maschinenstundensätze (im Rahmen der differenzierten Zuschlagskalkulation) berechnet?
Die Kalkulation mit Maschinenstundensätzen ist eine Verfeinerung der differenzierten Zuschlagskalkulation:
In dem oben dargestellten Schema der differenzierten Zuschlagskalkulation wurden in Zeile 2 die Fertigungsgemeinkosten als Zuschlag auf Basis der Fertigungseinzelkosten berechnet:
Bisher:
| Fertigungseinzelkosten (z. B. Fertigungslöhne) | |
| + | Fertigungsgemeinkosten |
| = | Fertigungskosten |
Bei dieser Berechnungsweise wird übersehen, dass die Fertigungsgemeinkosten bei einem hohen Automatisierungsgrad nur noch wenig von den Fertigungslöhnen beeinflusst sind, sondern vielmehr vom Maschineneinsatz verursacht werden. Von daher sind die Fertigungslöhne bei zunehmender Automatisierung nicht mehr als Zuschlagsgrundlage geeignet.
Man löst dieses Problem dadurch, indem die Fertigungsgemeinkosten aufgeteilt werden in maschinenabhängige und maschinenunabhängige Fertigungsgemeinkosten.
Die maschinenunabhängigen Fertigungsgemeinkosten bezeichnet man als „Restgemeinkosten“; als Zuschlagsgrundlage werden die Fertigungslöhne genommen.
Bei den maschinenabhängigen Fertigungsgemeinkosten werden als Zuschlagsgrundlage die Maschinenlaufstunden genommen. Es gilt:
$$Maschinenstundensatz = \frac{maschinenabhängige\; Fertigungsgemeinkosten}{Maschinenlaufstunden}$$
Das bisher verwendete Kalkulationsschema (vgl. Zeile 2) modifiziert sich. Es gilt:
Neu:
Fertigungslöhne + Restgemeinkosten (in % der Fertigungslöhne) + Maschinenkosten (Laufzeit des Auftrages • Maschinenstundensatz) = Fertigungskosten
Beispiele für maschinenabhängige Fertigungsgemeinkosten:
Kalkulatorische Abschreibung (AfA; Absetzung für Abnutzung)
kalkulatorische Zinsen
Energiekosten
Raumkosten
Instandhaltung, Werkzeuge.
Hinweis
Beachten Sie bitte, dass bei der kalkulatorischen AfA die Wiederbeschaffungskosten (WW; falls vorhanden) und bei den kalkulatorischen Zinsen die Anschaffungskosten (AW) als Bezugsbasis genommen werden. Ein evt. Restwert (RW) ist dabei zu berücksichtigen (Zinsen = (AW + RW) : 2 • p/100; AfA = (WW – RW) : n). Außerdem sind bei der Berechnung der maschinenabhängigen Kosten die Zeiträume einheitlich zu wählen (z. B. pro Jahr, pro Monat, pro Laufstunde).
Beispiel
Zuschlagskalkulation mit Maschinenstundensatz
Auf einer NC-Maschine wird ein Werkstück bearbeitet. Die Bearbeitungsdauer beträgt 86 Minuten; der Materialverbrauch liegt bei 160 €. Der anteilige Fertigungslohn für die Bearbeitung beträgt 40 € (Einrichten, Nacharbeit). Es sind Materialgemeinkosten von 80 % und Restgemeinkosten von 60 % zu berücksichtigen. Zu kalkulieren sind die Herstellkosten der Fertigung.
1. Schritt: Berechnung des Maschinenstundensatzes
Zur Berechnung des Maschinenstundensatzes wird auf folgende Daten der vergangenen Abrechnungsperiode zurückgegriffen:
| ► Anschaffungskosten der NC-Maschine: | 100.000 € | |
| ► Wiederbeschaffungskosten der NC-Maschine: | 120.000 € | |
| ► Nutzungsdauer der NC-Maschine: | 10 Jahre | |
| ► kalkulatorische Abschreibung: | linear | |
| ► kalkulatorische Zinsen: | 6 % vom halben Anschaffungswert | |
| ► Instandhaltungskosten: | 2.000 € p. a. | |
| ► Raumkosten: | ||
| – Raumbedarf: | 20 m2 | |
| – Verrechnungssatz je m2: | 10 €/m2/Monat | |
| ► Energiekosten: | ||
| – Energieentnahme der NC-Maschine: | 11 Kwh | |
| – Verbrauchskosten: | 0,12 €/Kwh | |
| – Jahresgrundgebühr: | 220 € | |
| ► Werkzeugkosten: | 6.000 € p. a., Festbetrag | |
| ► Laufzeit der NC-Maschine: | 1.800 Std. p. a. | |
Berechnung (vgl. dazu ausführlich: 4.1.5/01. Ermittlung der Kostenarten):
$$Kalkulatorische\; Zinsen = \frac{Anschaffungskosten + Restwert}{2} \cdot \frac{Zinssatz}{100}$$
$$= \frac{100.000 + 0}{2} \cdot \frac{6}{100} = 3.000 €$$
$$Kalkulatorische\; Abschreibung = \frac{Wiederbeschaffungskosten – Restwert}{Nutzungsdauer}$$
$$= \frac{120.000 – 0}{10} = 12.000 €$$
$$Raumkosten = Raumbedarf \cdot Verrechnungssatz/m^{2}/Monat \cdot 12 Monate$$
$$= 20\; m^{2} \cdot 10 €/m^{2}/Mon. \cdot 12\; Mon. = 2.400 €$$
$$Energiekosten = Energieverbrauch/Std. \cdot €/Kwh \cdot Laufleistung\; p. a. + Grundgebühr$$
$$= 11\; kwh * 0,12 €/Kwh \cdot 1.800\; Std.\; p. a. + 220 € = 2.596 €$$
$$Instandhaltungskosten = Festbetrag\; p. a. = 2.000 €$$
$$Werkzeugkosten = Festbetrag\; p. a. = 6.000 €$$
Daraus ergibt sich folgender Maschinenstundensatz:
$$Maschinenstundensatz = \frac{maschinenabhängige\; Fertigungsgemeinkosten}{Maschinenlaufstunden}$$
$$= \frac{27.996 €}{1.800\; Std.} = 15,55 €/Std.$$
lfd. Nr. maschinenabhängige Fertigungsgemeinkosten € p. a. 1 kalk. Zinsen 3.000 2 kalk. Abschreibung 12.000 3 Raumkosten 2.400 4 Energiekosten 2.596 5 Instandhaltungskosten 2.000 6 Werkzeugkosten 6.000 ∑ 27.996 Maschinenstundensatz = 27.996 € : 1.800 Std. = 15,55 €/Std. 2. Schritt: Kalkulation der Herstellkosten der Fertigung
Materialeinzelkosten 160,00 + Materialgemeinkosten 80 % 128,00 = Materialkosten 288,00 Fertigungslöhne 40,00 + Restgemeinkosten 60 % 24,00 = Maschinenkosten 86 min • 15,55 €/Std. : 60 min 22,29 = Fertigungskosten 86,29 Herstellkosten der Fertigung 374,29 Im vorliegenden Fall gilt:
$$Herstellkosten\; der\; Fertigung/Erzeugung = Herstellkosten\; des\; Umsatzes$$
08. Wie wird der Minutensatz bei der Kalkulation mit Maschinenstundensätzen ermittelt?
Der Maschinenstundensatz bezieht sich auf 60 Minuten. Der Minutensatz der Maschinenkosten ist:
$$Minutensatz = \frac{Maschinenstundensatz\; €/Std.}{60\; min/Std.}$$
$$z. B.: = 15,55\; :\; 60 = 0,2592 €/min$$
Für die auftragsbezogenen Maschinenkosten gilt:
$$Maschinenkosten_{Auftrag} = Minutensatz \cdot Belegungszeit$$
$$z. B.: = 0,2592 €/min \cdot 86\; min = 22,29 €$$
Weitere interessante Inhalte zum Thema
-
Kalkulation von Kostenträgern durchführen
Vielleicht ist für Sie auch das Thema Kalkulation von Kostenträgern durchführen (Durchführen von Kosten- und Leistungsrechnung) aus unserem Online-Kurs Steuern und überwachen betriebswirtschaftlicher Prozesse interessant.