Inhaltsverzeichnis
- 01. Welcher grundsätzliche Unterschied besteht zwischen den Kennzahlen „Produktivität, Wirtschaftlichkeit und Rentabilität“?
- 02. Welches Schema hat das Kennzahlensystem nach Du Pont (ROI)?
- 03. Welchen Zweck hat die Kostenvergleichsrechnung?
- 04. Wie wird die Kostenvergleichsrechnung durchgeführt?
- 05. Welche Varianten der Kostenvergleichsrechnung sind vorherrschend?
- 27.000
- 24.400
- 26.200
- 23.550
- 95.000
- 12.660
- 06. Wie wird die Gewinnvergleichsrechnung durchgeführt?
- 66.200
- 81.600
- 84.000
- 17.800
- 26.400
- 07. Welchen Aussagewert hat die Rentabilitätsvergleichsrechnung?
- 08. Welchen Aussagewert hat die Amortisationsvergleichsrechnung?
- 80.000
01. Welcher grundsätzliche Unterschied besteht zwischen den Kennzahlen „Produktivität, Wirtschaftlichkeit und Rentabilität“?
Hinweis
Die Darstellung der Unterschiede zwischen diesen Kennzahlen erscheint den Autoren notwendig, weil die Abgrenzung und Anwendung in der Praxis nicht immer „sauber“ ist.
A. Produktivität
$$Produktivität = \frac{Mengengröße}{Mengengröße}$$
Die Produktivität ist eine Mengenkennziffer. Sie zeigt die mengenmäßige Ergiebigkeit eines Faktoreinsatzes (z. B. Anzahl der Maschinenstunden, Anzahl der Mitarbeiterstunden, Menge des verbrauchten Rohstoffes) zur erzeugten Menge (in Stückzahlen, in Einheiten u. Ä.). Als Einzelwert hat die Produktivität keine Aussagekraft; dies wird erst im Vergleich mit innerbetrieblichen Ergebnissen (z. B. der Vorperiode) oder im zwischenbetrieblichen Vergleich erreicht.
Wichtige Teilproduktivitäten sind:
A.1 Arbeitsproduktivität
$$Arbeitsproduktivität = \frac{Erzeugte\; Menge\; (Stk.,\; E)}{Arbeitsstunden}$$
A.2 Materialproduktivität
$$Materialproduktivität = \frac{Erzeugte\; Menge\; (Stk.,\; E)}{Materialeinsatz\; (t,\; kg,\; u. Ä.)}$$
A.3 Maschinenproduktivität
$$Maschinenproduktivität = \frac{Erzeugte\; Menge\; (Stk.,\; E)}{Maschinenstunden}$$
B. Wirtschaftlichkeit
$$Wirtschaftlichkeit = \frac{Leistungen}{Kosten}$$
oder
$$Wirtschaftlichkeit = \frac{Ertrag}{Aufwand}$$
Die Wirtschaftlichkeit ist eine Wertkennziffer. Sie misst die Einhaltung des ökonomischen Prinzips und ist der Quotient aus Leistungen und Kosten oder Ertrag und Aufwand.
C. Rentabilität
$$Rentabilität = \frac{Periodenerfolg}{gewählte\; Größe\; X} \cdot 100$$
Die Rentabilität (auch: Rendite) ist eine Wertkennziffer und misst die Ergiebigkeit des Kapitaleinsatzes (oder des Umsatzes) zum Periodenerfolg. Als Größen für den Periodenerfolg werden verwendet: Gewinn, Return (Gewinn + Fremdkapitalzinsen), Cashflow.
Es werden vor allem folgende Rentabilitätszahlen betrachtet:
C.1Eigenkapitalrentabilität
$$Eigenkapitalrentabilität = \frac{Gewinn}{Eigenkapital} \cdot 100$$
Zeigt die Beziehung von Gewinn (= Jahresüberschuss) zu Eigenkapital = Grundkapital + offene Rücklagen).
C.2 Gesamtkapitalrentabilität
$$Gesamtkapitalrentabilität = \frac{Gewinn + Fremdkapitalzinsen}{Gesamtkapital} \cdot 100$$
Zeigt die Beziehung von Gewinn und Fremdkapitalzinsen zu Gesamtkapital; die Verzinsung des Gesamtkapitals zeigt die Leistungsfähigkeit des Unternehmens (vgl. Leverage-Effekt). Aus dieser Größe lässt sich durch Erweiterung des Quotienten mit dem Faktor Umsatz der Return on Investment (ROI) ableiten.
C.3 Umsatzrentabilität
$$Umsatzrentabilität = \frac{Gewinn}{Umsatzerlöse} \cdot 100$$
Zeigt die relative Erfolgssituation des Unternehmens: Niedrige Umsatzrenditen bedeuten i. d. R. eine ungünstige wirtschaftliche Entwicklung (siehe: Branchenvergleich und Zeitvergleich über mehrere Jahre).
C.4 ROI Return on Investment
$$ROI = \frac{Return \cdot 100}{Umsatz} \cdot umsatzinvestiertes\; Kapital$$
$$ROI = Umsatzrendite \cdot Kapitalumschlag$$
Rein rechnerisch ist der ROI (Return on Investment) identisch mit der Gesamtkapitalrentabilität. Die Aufspaltung in zwei Kennzahlen erlaubt eine verbesserte Analyse der Ursachen für Verbesserungen/Verschlechterungen der Gesamtkapitalrendite (vgl. Kennzahlensystem nach Du Pont).
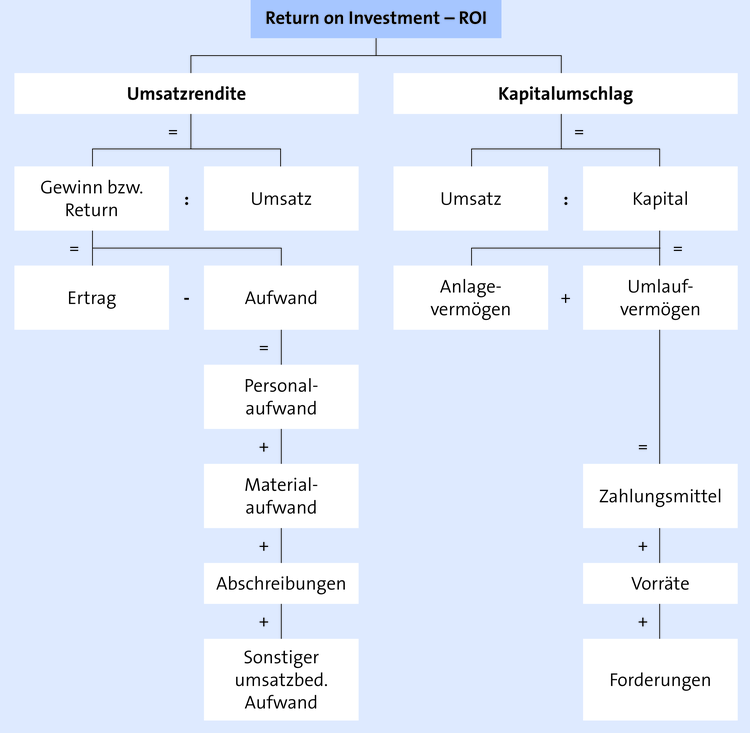
02. Welches Schema hat das Kennzahlensystem nach Du Pont (ROI)?
Die Gesamtkapitalrentabilität ist definiert als:
$$Gesamtkapitalrentabilität = \frac{Gewinn + Fremdkapitalzinsen}{Gesamtkapital} \cdot 100$$
$$Gesamtkapitalrentabilität = \frac{Return\; }{Gesamtkapital} \cdot 100$$
$$Gesamtkapitalrentabilität = \frac{R}{GK} \cdot 100$$
Durch die Erweiterung des Quotienten [R • 100 : GK] mit der Größe Umsatz (U) entsteht eine differenzierte Berechnungsgröße, die sich aus den Faktoren [Umsatzrendite] und [Kapitalumschlag] zusammensetzt:
$$ROI = \frac{R \cdot 100 \cdot U}{GK cdot U}$$
$$ROI = \frac{R \cdot 100}{U} \cdot \frac{U}{GK}$$
$$Return\; on\; Investment\; (ROI) = \frac{Return \cdot 100}{Umsatz} \cdot \frac{Umsatz \cdot 100}{Kapitaleinsatz}$$
$$Return\; on\; Investment\; (ROI) = Umsatzrendite \cdot Kapitalumschlag$$
Das Kennzahlensystem ROI ist vom amerikanischen Chemieunternehmen Du Pont entwickelt worden. Es ermöglicht – im Gegensatz zur Kennzahl Gesamtkapitalrentabilität – die Aussage, ob Veränderungen in der Verzinsung des eingesetzten Kapitals auf einer Veränderung der Umsatzrendite oder des Kapitalumschlags beruhen.
Der ROI lässt sich auf folgendes Schema erweitern (Kennzahlensystem nach Du Pont):
Aus dem Kennzahlensystem von Du Pont lassen sich Maßnahmen zur Verbesserung des ROI ableiten; die nachfolgenden Beispiele gelten unter der Voraussetzung, dass alle anderen Größen jeweils unverändert bleiben:
Der ROI steigt, wenn
die Umsatzrendite steigt
der Kapitalumschlag steigt
der Kapitaleinsatz sich verringert
die Forderungsbestände sinken
der Gewinn steigt
der Aufwand sinkt
die Verbindlichkeiten steigen.
03. Welchen Zweck hat die Kostenvergleichsrechnung?
Die Kostenvergleichsrechnung hat den Zweck, die wirtschaftliche Zweckmäßigkeit von Investitionen zu überprüfen. Es werden die Kosten von zwei oder mehreren Investitionsobjekten/Verfahren gegenübergestellt und verglichen. Dasjenige Investitionsobjekt/Verfahren ist vorteilhafter, bei dem die Kosten geringer sind. Die Kostenvergleichsrechnung gehört zu den sog. statischen Verfahren der Investitionsrechnung.
04. Wie wird die Kostenvergleichsrechnung durchgeführt?
Ist die genutzte Kapazität (nicht die technische Kapazität) von zwei Anlagen gleich groß, wird ein Vergleich der Kosten pro Abrechnungsperiode oder pro Stück durchgeführt; es werden alle relevanten Kosten, die nicht identisch sind, gegenübergestellt.
Werden die Anlagen in unterschiedlicher Höhe genutzt, müssen die Stückkosten miteinander verglichen werden.
Relevant sind folgende Kostenkomponenten:
Betriebskosten (Material, Personal, Energie, Raumkosten) – unterschieden in:
Kf fixe Kosten Kv variable Kosten kv variable Kosten pro Stück bzw. pro Leistungseinheit Kalkulatorische Zinsen:
Sie werden auf das während der Nutzungsdauer durchschnittlich gebundene Kapital bezogen.
$$Z = \frac{AW + RW}{2} \cdot i$$
AW = Anschaffungswert RW = Restwert i = Kalkulationszins in Dezimalform Kalkulatorische Abschreibung:
Der Kapitalverzehr wird auf ein Jahr bezogen (lineare AfA).
$$AfA = \frac{AW – RW}{n}$$
n = Nutzungsdauer in Jahren
05. Welche Varianten der Kostenvergleichsrechnung sind vorherrschend?
| Kostenvergleichsrechnung | ||
| Varianten | Situation | Auswahlentscheidung |
| Variante 1 | Kostenvergleich identischer Anlagen: Die Kapazität der betrachteten Anlagen ist gleich. | Kostenvergleich pro Periode |
| Variante 2 | Kostenvergleich nicht identischer Anlagen: Die Kapazität der betrachteten Anlagen ist verschieden. Es wird eine Maximalkapazitätsausnutzung unterstellt. | Kostenvergleich pro Leistungseinheit |
| Variante 3 | Kritische Menge: Die Kapazität der betrachteten Anlagen ist verschieden; der zukünftige Leistungsgrad ist ungewiss. | Bestimmung der kritischen Menge durch Vergleich der Gesamtkosten, die in fixe und variable Kosten zerlegt werden. |
| Variante 4 | Kostenvergleich bei der Ersatzinvestition einer Anlage unter Beachtung des Restwertes der alten Anlage. | KostenNeuanlage Altanlage
|
Beispiel
Beispiel zu Variante 1: Zwei identische Anlagen, ohne Restwert (in €)
| Kalkulationsangaben | Abk. | Anlage I | Anlage II | ||
| Anschaffungswert (in €) | AW | 50.000 | 80.000 | ||
| Leistung, Einheiten pro Jahr | E | 40.000 | 40.000 | ||
| Nutzungsdauer | n | 5 | 8 | ||
| kalkulatorischer Zinssatz | p | 8 % | |||
| i | 0,08 | ||||
| Restwert | RW | 0 | |||
| Betriebskosten | |||||
| Lohnkosten | 8.000 | 6.000 | |||
| Instandhaltung | 3.500 | 2.000 | |||
| Energie und Materialkosten | 2.500 | 2.000 | |||
| Raumkosten | 1.000 | 1.200 | |||
| Kalkulatorische AfA: Anlage 1: (50.000 – 0) : 5 Anlage 2: (80.000 – 0) : 8 | $$\frac{AW – RW}{n}$$ | 10.000 | 10.000 | ||
| Kalkulatorische Zinsen: Anlage 1: (50.000 + 0) : 2 • 0,08 Anlage 2: (80.000 + 0) : 2 • 0,08 | $$\frac{AW + RW}{2}* i$$ | 2.000 | 3.200 | ||
| Gesamtkosten | 27.000 | 24.400 | |||
| Kostenvorteil | 2.600 | ||||
Ergebnis: Anlage II ist vorteilhafter. Dabei muss in der Praxis beachtet werden, dass bei geringen Kostenunterschieden der Investitionsalternativen kein „Automatismus“ der Entscheidung gilt. Ggf. muss die Kostenvergleichsrechnung erneut unter Best-case- und Worst-case-Bedingungen durchgeführt werden, denn das Ergebnis der Rechnung ist nur so zuverlässig wie die Prämissen (K, n, RW, Kapazität) Gültigkeit haben.
Beispiel zu Variante 2:
Zwei Anlagen mit unterschiedlicher Kapazität mit Restwert (in €); der Restwert > 0 reduziert die kalkulatorische AfA und erhöht die kalkulatorischen Zinsen; zu Übungszwecken werden ansonsten die gleichen Daten wie im Beispiel zu Variante 1 unterstellt.
| Kalkulationsangaben | Abk. | Anlage I | Anlage II | ||
| Anschaffungswert (in €) | AW | 50.000 | 80.000 | ||
| Leistung, Einheiten pro Jahr | E | 40.000 | 50.000 | ||
| Nutzungsdauer | n | 5 | 8 | ||
| kalkulatorischer Zinssatz | p | 8 % | |||
| i | 0,08 | ||||
| Restwert | RW | 5.000 | 10.000 | ||
| Betriebskosten | |||||
| Lohnkosten | 8.000 | 6.000 | |||
| Instandhaltung | 3.500 | 2.000 | |||
| Energie und Materialkosten | 2.500 | 2.000 | |||
| Raumkosten | 1.000 | 1.200 | |||
| Kalkulatorische AfA: Anlage I: (50.000 – 5.000) : 5 Anlage II: (80.000 – 10.000) : 8 | $$\frac{AW – RW}{n}$$ | 9.000 | 8.750 | ||
| Kalkulatorische Zinsen: Anlage I: (50.000 + 5.000) : 2 • 0,08 Anlage II: (80.000 + 10.000) : 2 • 0,08 | $$\frac{AW + RW}{2}* i$$ | 2.200 | 3.600 | ||
| Gesamtkosten | 26.200 | 23.550 | |||
| Kosten pro Einheit | 0,66 | 0,47 | |||
| Kostenvorteil pro Einheit | 0,19 | ||||
Ergebnis: Anlage II ist vorteilhafter.
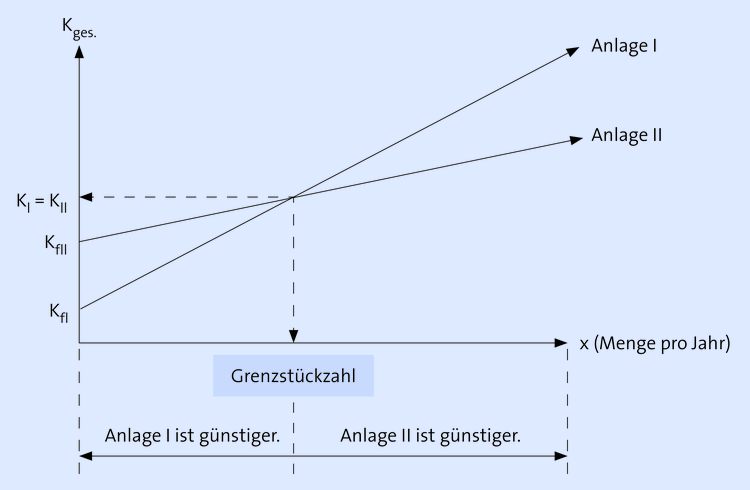
Beispiel zu Variante 3:
Vergleich von zwei Produktionsverfahren und Berechnung der Grenzstückzahl; Fragestellung: Welches Produktionsverfahren ist bei gegebener Losgröße kostengünstiger bzw. bei welcher Menge (Grenzstückzahl) sind beide Verfahren kostengleich?
| Verfahren I | Verfahren II | ||
| Rüsten | Vorgabezeit | 0,5 Std. | 6,5 Std. |
| Stundensatz | 20 € | 42 € | |
| Fertigen | Vorgabezeit | 2,2 min/E | 0,8 min/E |
| Stundensatz | 24 € | 48 € | |
1. Schritt: Errechnen der variablen Stückkosten:
Verfahren I:
| 60 min | – | 24 € |
| 2,2 min | – | kvI |
| → kvI | = | 24 • 2,2 : 60 |
| = | 0,88 € |
Verfahren II:
analog
→ kvII = 0,64 €
2. Schritt: Die Kosten für beide Verfahren werden gleichgesetzt; mit x wird die Stückzahl bezeichnet:
| 0,5 • 20 + x • 0,88 | = | 6,5 • 42 + x • 0,64 | |
| → | x | = | rd. 1.096 Stück |
In Worten: Bei rd. 1.096 Stück (= Grenzstückzahl) sind die Kosten beider Verfahren gleich. Oberhalb der Grenzstückzahl ist Verfahren II wirtschaftlicher (Vorteil der variablen Stückkosten), unterhalb der Grenzstückzahl ist Verfahren I günstiger (Vorteil der geringeren Fixkosten).
Allgemein gilt:
rechnerisch:
$$Grenzstückzahl = \frac{Fixkosten_{II} – Fixkosten_{I}}{var.\; Stückkosten_{I} – var.\; Stückkosten_{II}}$$
$$x = \frac{K_{fII} – K_{fI}}{k_{vI} – k_{vII}}\; bzw.\; \frac{K_{fI} – K_{fII}}{k_{vII} – k_{vI}}$$
grafisch:
Beispiel zu Verfahren 4: Kostenvergleich bei Ersatzinvestition
Während der laufenden Nutzung einer Anlage (Altanlage) wird die Fragestellung untersucht, ob es günstiger ist, die Altanlage weiterhin zu nutzen oder durch eine Neuanlage zu ersetzen und wann der optimale Ersatzzeitpunkt vorliegt. Es gibt zwei Berechnungsvarianten:
Bruttomethode:
Die Kapital- und Betriebskosten der Altanlage werden mit den Kapital- und Betriebskosten der Neuanlage verglichen.
Nettomethode:
Es werden nur die Betriebskosten der Altanlage mit den Kapital- und Betriebskosten der Neuanlage verglichen. Diese Methode wird in jüngster Zeit favorisiert.
Ist davon auszugehen, dass für die Altanlage ein Liquidationserlös L erzielt werden kann, so ist er bei dem Kostenvergleich zu berücksichtigen. Begründung: Der Liquidationserlös sinkt mit zunehmender Nutzungsdauer. Man „belastet“ also im Kostenvergleich die Altanlage mit der Differenz des Liquidationserlöses am Beginn und am Ende der Vergleichsperiode bezogen auf die Restnutzungsdauer:
$$L = \frac{RW_{A} – RW_{E}}{RND}$$
| RWA | = Restwert am Anfang der Vergleichsperiode |
| RWE | = Restwert am Ende der Vergleichsperiode |
| RND | = Restnutzungsdauer |
| L | = durchschnittliche Verringerung des Liquidationserlöses (ø Restwertminderung) |
Beispiel
Die Altanlage hat eine geplante Nutzungsdauer von 10 Jahren. Nach 6 Jahren soll die Vorteilhaftigkeit einer Ersatzinvestition geprüft werden. Der Liquidationserlös am Ende des 6. Jahres wird mit 20.000 €, am Ende der Nutzungsdauer mit 6.000 € angenommen:
$$L = \frac{20.000 – 6.000}{4} = 3.500 €$$
Die kalkulatorischen Zinsen für die Altanlage beziehen sich auf das noch gebundene Kapital, wenn die Altanlage weiter genutzt wird. Sie sind abhängig vom Zinssatz und den Liquidationserlösen am Anfang und am Ende des Vergleichszeitraums:
$$Z = \frac{RW_{A} + RW_{E}}{2} \cdot i$$
| RWA | = Restwert am Anfang der Vergleichsperiode |
| RWE | = Restwert am Ende der Vergleichsperiode |
| i | = Kalkulationszins in Dezimalform |
Beispiel: Es wird ein Zinssatz von 8 % unterstellt.
$$Z = \frac{20.000 + 6.000}{2} \cdot 0,08 = 1.040 €$$
Das nachfolgende Beispiel zeigt einen Gesamtkostenvergleich bei alternativer Ersatzinvestition (Bruttomethode):
| Kalkulationsangaben | Abk. | Altanlage | Neuanlage | ||
| Anschaffungswert (in €) | AW | 150.000 | 200.000 | ||
| Leistung, Einheiten pro Jahr | E | 5.000 | |||
| Nutzungsdauer | n | 8 | |||
| kalkulatorischer Zinssatz | p | 8 % | |||
| Restwert am Anfang der Vergleichsperiode | RWA | 31.000 | – | ||
| Restwert am Ende der Vergleichsperiode | RWE | 10.000 | 20.000 | ||
| Betriebskosten | |||||
| Lohnkosten | 40.000 | 40.000 | |||
| Energie und Materialkosten | 30.000 | 25.000 | |||
| Sonstige variable Kosten | 15.000 | 12.000 | |||
| Fixkosten ohne AfA und Zinsen | 20.000 | 18.000 | |||
| Zwischensumme | 105.000 | 95.000 | |||
| Ø Restwertminderung | (31.000 – 10.000) : 3 | 7.000 | – | ||
| Kalkulatorische AfA: | (200.000 – 20.000) : 8 | – | 22.500 | ||
| Kalkulatorische Zinsen: | Altanlage: (31.000 + 10.000) : 2 • 0,08 | 1.640 | – | ||
| Neuanlage: (200.000 + 20.000) : 2 • 0,08 | – | 8.800 | |||
| Gesamtkosten | 113.640 | 126.300 | |||
| Kostenvorteil | 12.660 | ||||
Ergebnis: Es ist zurzeit vorteilhafter, die Altanlage weiter zu nutzen.
06. Wie wird die Gewinnvergleichsrechnung durchgeführt?
Die Gewinnvergleichsrechnung ergänzt die Kostenvergleichsrechnung um die Größe „Erlöse“ und ist damit aussagefähiger. Zu wählen ist diejenige Investition, die den größten durchschnittlichen Gewinn erzielt. Bei gleichen Erlösen pro Leistungseinheit für beide Investitionsobjekte kommt sie selbstverständlich zur gleichen Bewertung wie die Kostenvergleichsrechnung. Die Gewinnvergleichsrechnung setzt voraus, dass die erzielbaren Erlöse je Investitionsalternative über den gesamten Planungszeitraum ermittelt werden können.
Der Gewinn ergibt sich als Differenz zwischen den Kosten und den Umsatzerlösen:
$$G = U – K$$
$$G = x \cdot p – K_{f} – x \cdot k_{v}$$
| U | = Umsatz |
| K | = Gesamtkosten |
| Kf | = Fixkosten |
| kv | = variable Stückkosten |
| x | = Menge |
| p | = Verkaufspreis |
Bei einer Einzelinvestition gilt:
Die Vorteilhaftigkeit ist gegeben, wenn der Gewinn positiv ist bzw. ein bestimmter Mindestgewinn erreicht wird:
G > 0 bzw. G ≥ Mindestgewinn
Beim Vergleich von zwei oder mehreren Investitionsobjekten gilt:
Es wird die Investition mit dem größeren Gewinn gewählt.
GI > GII → Anlage I ist vorteilhafter.
GII > GI → Anlage II ist vorteilhafter.
Hier klicken zum AusklappenBeispiel
Kalkulationsangaben Anlage I Anlage II Anschaffungswert 50.000 80.000 Leistung, Einheiten pro Jahr 4.000 4.500 Nutzungsdauer 5 7 kalkulatorischer Zinssatz 8 % Restwert 5.000 10.000 Verkaufspreis pro Stück 21 24 Betriebskosten Kalkulatorische AfA (50.000 – 5.000) : 5 9.000 (80.000 – 10.000) : 7 10.000 Kalkulatorische Zinsen (50.000 + 5.000) : 2 • 0,08 2.200 (80.000 + 10.000) : 2 • 0,08 3.600 Sonstige Fixkosten/Jahr 15.000 18.000 Variable Kosten/Jahr 40.000 50.000 Gesamtkosten/Jahr 66.200
81.600
Umsatzerlöse/Jahr 4.000 • 21 84.000
4.500 • 24 108.000 Gewinn/Jahr 17.800
26.400
Gewinnvorteil/Jahr 8.600 Ergebnis: Anlage II hat den größeren Gewinn und ist damit vorteilhafter.
Bei der Lösung eines Ersatzproblems (optimaler Ersatzzeitpunkt) werden die Erlöse der alten Anlage denen der neuen gegenübergestellt (vgl. Kostenvergleichsrechnung; Berücksichtigung der Restwertminderung der alten Anlage).
07. Welchen Aussagewert hat die Rentabilitätsvergleichsrechnung?
Die Rentabilitätsrechnung baut auf den Ergebnissen der Kostenvergleichs- bzw. Gewinnvergleichsrechnung auf und berücksichtigt dabei den erforderlichen Kapitaleinsatz alternativer Investitionsobjekte. Während also die Kostenvergleichsrechnung (nur) eine relative Vorteilhaftigkeit beim Vergleich alternativer Investitionsobjekte bietet, ermöglicht die Rentabilitätsvergleichsrechnung die Ermittlung der absoluten Vorteilhaftigkeit.
Die Rentabilitätsrechnung vergleicht die durchschnittliche jährliche Verzinsung des eingesetzten Kapitals alternativer Investitionsobjekte. Es gilt:
$$Rentabilität = \frac{Return}{ø\; Kapitaleinsatz} \cdot 100$$
Die Rentabilität R kann unterschiedlich definiert werden, z. B.
als Rentabilität des Eigenkapitals, des Fremdkapitals, des Gesamtkapitals und als Umsatzrentabilität
oder
als Return on Investment, ROI.
Die Größe „Return“ (Kapitalrückfluss) kann je nach Besonderheit des Betriebes oder des Sachverhaltes unterschiedlich definiert sein, z. B. als [Gewinn], [Gewinn + Abschreibungen], [Cashflow], [Erträge – Kosten].
Bei Verwendung der Größe „Gewinn“ wird nach vorherrschender Meinung der „Gewinn vor Zinsen“ verwendet (keine Verminderung des Gewinns um die kalkulatorischen Zinsen):
$$Rentabilität = \frac{Gewinn\; (vor\; Zinsen)}{ø\; Kapitaleinsatz} \cdot 100$$
Der durchschnittliche Kapitaleinsatz wird i. d. R. wie folgt ermittelt:
Berechnung des ø Kapitaleinsatzes Vermögenswert Wertansatz Nicht abnutzbare Anlagegüter Anschaffungswert Umlaufvermögen Abnutzbare Anlagegüter $$\frac{Anschaffungswert + Restwert}{2}$$
oder: $$\frac{Wiederbeschaffungswert + Restwert}{2}$$
Bei einer Einzelinvestition gilt:
Die Vorteilhaftigkeit ist gegeben, wenn die Rentabilität R eine bestimmte Mindestverzinsung erreicht oder überschreitet.
R ≥ Mindestverzinsung
Beim Vergleich von zwei oder mehreren Investitionsobjekten gilt:
Es wird die Investition mit der höheren Rentabilität gewählt. Auf Objekte, deren Rendite die geforderte Mindestverzinsung nicht erreicht, sollte verzichtet werden.
RI > RII → Anlage I ist vorteilhafter.
RII > RI → Anlage II ist vorteilhafter.
Hier klicken zum AusklappenBeispiel
Es werden zwei Anlagen miteinander verglichen; es liegen folgende Zahlen vor (in €):
Anlage I Anlage II Anschaffungskosten 100.000 200.000 Wiederbeschaffungswert 151.336 200.000 Restwert 0 20.000 Abschreibungen 21.182 20.000 Periodengewinn vor Steuern 13.905 21.525 $$R_{I} = \frac{13.905}{75.668} \cdot 100 = 18,38 \%$$
$$R_{II} = \frac{21.525}{110.000} \cdot 100 = 19,57 \%$$
Als „Return“ wird hier der Periodengewinn der Anlage genommen; der „Ø Kapitaleinsatz“ ist gleich „Wiederbeschaffungswert plus Restwert : 2“ (Vergleichbarkeit des Kapitaleinsatzes).
Daraus folgt: RI II, d. h. die Anlage II ist vorteilhafter.
08. Welchen Aussagewert hat die Amortisationsvergleichsrechnung?
Die Amortisationsvergleichsrechnung (auch: Kapitalrückflussmethode, Payback-Methode/Payoff-Methode) gehört ebenfalls zu den statischen Verfahren der Investitionsrechnung und baut auch auf den Ergebnissen der Kostenvergleichs- bzw. Gewinnvergleichsrechnung auf.
Die Vorteilhaftigkeit einer Investition wird an der Kapitalrückflusszeit tw gemessen (= Amortisationszeit = die Zeit, in der das eingesetzte Kapital wieder in das Unternehmen zurückgeflossen ist). Je geringer die Kapitalrückflusszeit ist, desto vorteilhafter wird das Investitionsvorhaben beurteilt.
Bei einer Einzelinvestition gilt:
Die Vorteilhaftigkeit ist gegeben, wenn die Amortisationszeit tw einen bestimmten Zeitwert t* nicht überschreitet:
$$t_{w}\; ≤\; t*$$
Beim Vergleich von zwei oder mehreren Investitionsobjekten gilt:
Es wird die Investition mit der geringeren Kapitalrückflusszeit gewählt. Auf Objekte, deren Amortisationsdauer den geforderten Zeitwert t* überschreitet, sollte verzichtet werden.
twI wII → Anlage I ist vorteilhafter.
twII wI → Anlage II ist vorteilhafter.
Man unterscheidet zwei Berechnungsmethoden:
Durchschnittmethode:
$$Kapitalrückflusszeit\; (Jahre) = \frac{Kapitaleinsatz}{ø\; Return}$$
Als Kapitaleinsatz wird i. d. R. der Anschaffungswert AW vermindert um den Restwert RW verwendet.
In der Regel wird als Größe für den ø Return die Summe aus [Ø Gewinn + jährliche Abschreibungen] genommen.
Es gilt also:
$$Kapitalrückflusszeit\; (Jahre) = \frac{Anschaffungswert – Restwert}{ø\; Gewinn + Abschreibungen\; p. a.}$$
$$t_{w} = \frac{AW – RW}{G + AfA}$$
Hier klicken zum AusklappenBeispiel
Vergleich von zwei Investitionsobjekten
Es wird noch einmal das Zahlengerüst aus dem Beispiel „Rentabilitätsvergleich“ genommen.
$$t_{wI} = \frac{100.000 – 0}{13.905 + 21.182} = 2,85\; Jahre$$
$$t_{wII} = \frac{200.000 – 20.000}{21.525 + 20.000} = 4,33\; Jahre$$
Ergebnis: twI wII, d. h. aus der Sicht der Kapitalrücklaufzeit ist die Anlage I vorteilhafter (bitte betrachten Sie oben nochmals den Rentabilitätsvergleich der beiden Anlagen).
Kumulationsmethode:
Die geschätzten jährlichen Zahlungsströme werden solange aufaddiert, bis der Kapitaleinsatz erreicht ist. Die Kumulationsrechnung ist genauer, da sie nicht mit einem repräsentativen Mittelwert rechnet, sondern die geschätzten Rückflüsse den einzelnen Jahren gesondert zuordnet.
Hier klicken zum AusklappenBeispiel
Für eine Einzelinvestition soll gelten: AW = 80.000; RW = 0; n = 5 Es werden folgende Rückflüsse pro Jahr geschätzt:
Jahr t1 t2 t3 t4 t5 Kapitalrückfluss 10.000 25.000 45.000 70.000 100.000 Kapitalrückfluss, kumuliert 10.000 35.000 80.000
150.000 250.000 Nach der Kumulationsmethode ergibt sich:
$$t_{w} = t_{3}$$
Nach der Durchschnittsmethode ist der durchschnittliche Kapitaleinsatz 50.000 (= 250.000 : 5). Daraus ergibt sich:
$$t_{w} = \frac{80.000}{50.000} = 1,6\; Jahre$$
Dies bedeutet: Wenn die Kapitalrückflüsse eine ungleichmäßige Verteilung innerhalb des Nutzungszeitraums aufweisen, kann die Durchschnittsmethode zu Fehlentscheidungen führen.