Inhaltsverzeichnis
- 01. Wie unterscheiden sich die beschreibende und die beurteilende Statistik (Einsatzbereiche statistischer Methoden)?
- 02. Welche Begriffe werden in der Fachsprache der Statistik verwendet?
- 03. Zur Wiederholung: In welchen Schritten erfolgt die Lösung statistischer Fragestellungen?
- 04. Zur Wiederholung: Wie wird das statistische Zahlenmaterial aufbereitet?
- 05. In welchen Arbeitsschritten geht die technische Statistik vor (Grundmodelle)?
- 06. Wie erfolgt die Erfassung und Verarbeitung technischer Messwerte?
- 07. Lassen sich Fehler bei der Erfassung von Messwerten vermeiden?
01. Wie unterscheiden sich die beschreibende und die beurteilende Statistik (Einsatzbereiche statistischer Methoden)?
Beschreibende Statistik (deskriptive Statistik)
Ordnen von Daten
Darstellen von Daten (Tabellen, Diagramme)
Berechnung von Parametern (Mittelwerte, Streuungsmaße)
Beurteilende Statistik
Schließen von Stichproben auf die Grundgesamtheit
Formulieren und Prüfen von Hypothesen
Schätzen von Parametern.
02. Welche Begriffe werden in der Fachsprache der Statistik verwendet?
Dazu eine Auswahl häufig verwendeter Begriffe:
| Begriffe | Beispiele | |
| Grundgesamtheit | Als Grundgesamtheit (= statistische Masse) bezeichnet man die Gesamtheit der statistisch erfassten gleichartigen Elemente. | alle gefertigten Teile für Auftrag X, z. B. 3.500 Schrauben M8 × 40 |
| Bestandsmassen | sind diejenigen Massen, die sich auf einen Zeitpunkt beziehen. | 01.07. des Jahres |
| Bewegungsmassen | Bewegungsmassen beziehen sich auf einen bestimmten Zeitraum. | 01.01. bis 30.06. d. J. |
| Abgrenzung der Grundgesamtheit | Je nach Fragestellung ist die Grundgesamtheit abzugrenzen; vorherrschend sind folgende Abgrenzungsmerkmale: | |
|
| |
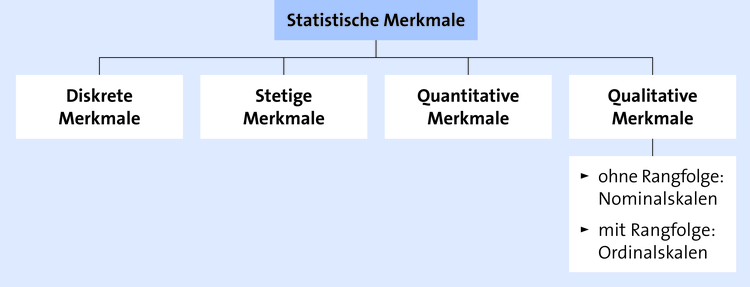
| Merkmal | Als Merkmal bezeichnet man die Eigenschaft, nach der in einer statistischen Erfassung gefragt wird. |
|
| Merkmalsausprägungen | nennt man die Werte, die ein bestimmtes-Merkmal haben kann. |
|
| Diskrete Merkmale | können nur einen Wert annehmen. |
|
| Stetige Merkmale | können jeden Wert annehmen. |
|
| Qualitative Merkmale | erfassen Eigenschaften/Qualitäten eines Merkmalsträgers |
|
| Quantitative Merkmale | sind Merkmale, deren Ausprägungen in Zahlen angegeben werden – mit Benennung der Maßeinheit. |
|
| Ordinalskala | Erfolgt eine Festlegung der Rangfolge der Merkmalsausprägungen, so spricht man von Ordinalskalen … |
|
| Nominalskalen | … ansonsten von Nominalskalen. |
|
| Häufigkeit | Anzahl der Messwerte einer Messreihe zu einem bestimmten Messwert xi. | |
03. Zur Wiederholung: In welchen Schritten erfolgt die Lösung statistischer Fragestellungen?
Die Lösung statischer Fragestellungen erfolgt generell in vier Schritten:
Analyse der Ausgangssituation
Erfassen des Zahlenmaterials
Aufbereitung, d. h. Gruppierung und Auszählung der Daten und Fakten
Auswertung, d. h. Analyse des Zahlenmaterials nach methodischen Gesichtspunkten.
04. Zur Wiederholung: Wie wird das statistische Zahlenmaterial aufbereitet?
Das Zahlenmaterial kann erst dann ausgewertet und analysiert werden, wenn es in aufbereiteter Form vorliegt. Dazu werden die Merkmalsausprägungen geordnet – z. B. nach Geschlecht, Alter, Beruf, Region, gut/schlecht, Länge, Materialart usw.
Grundsätzliche Ordnungsprinzipien im Rahmen der Aufbereitung sind:
Ordnen des Zahlenmaterials in einer Nominalskala (qualitative Merkmale; xi = gut, xi = schlecht).
Ordnen des Zahlenmaterials in einer Kardinalskala (x1 = 1, x2 = 5, x3 = 7 …) oder einer Ordinalskala (xi = nicht ausreichend, xi = ausreichend, xi = befriedigend, xi = gut, …).
Unterscheidung in diskrete und stetige Merkmale.
Ggf. Aufbereitung in Form einer Klassenbildung (bei stetigen Merkmalen; xi ≤ 0, 0 > xi ≤ 10, 10 i ≤ 20, …).
Aufbereitung ungeordneter Reihen in geordnete Reihen.
Bildung absoluter und relativer Häufigkeiten (Verteilungen).
05. In welchen Arbeitsschritten geht die technische Statistik vor (Grundmodelle)?
Schritt: Formulierung des Problems
Hier klicken zum AusklappenBeispiel
In einem Stahl erzeugenden Unternehmen soll der angelieferte Koks auf seine Dichte hin überprüft werden. Der beauftragte Mitarbeiter erhält die Aufgabe, die durchschnittliche Dichte des gelieferten Kokses zu bestimmen.
Schritt: Planung des Experiments
Hier klicken zum AusklappenBeispiel
Da die Dichte der einzelnen Koksbrocken unterschiedlich ist, müsste der Mitarbeiter – genau genommen – alle Koksbrocken untersuchen und ihre Dichte bestimmen. Diese Vorgehensweise ist jedoch aus Kosten- und Zeitgründen nicht akzeptabel. Man wählt daher in der Praxis folgenden Weg: Der Mitarbeiter soll eine hinreichend große Anzahl von Koksbrocken zufällig auswählen und deren Dichte bestimmen (= Stichprobe).
Schritt: Durchführung des Experiments
Hier klicken zum AusklappenBeispiel
Der Mitarbeiter verfährt wie geplant. Diesen Vorgang des Auswählens und Messens der Koksbrocken nennt man in der Statistik ein Zufallsexperiment (kurz: Experiment). Die erhaltenen Messwerte werden als Stichprobe aus der Grundgesamtheit bezeichnet. Die Anzahl der ausgewählten und gemessenen Werte ist der Umfang der Stichprobe.
Schritt: Aufbereitung des experimentellen Ergebnisses und Berechnung von Maßzahlen
Hier klicken zum AusklappenBeispiel
Bei umfangreichen Untersuchungen mit vielen Zahlenwerten ist es erforderlich, die Ergebnisse tabellarisch und ggf. auch grafisch aufzubereiten. Außerdem werden Maßzahlen berechnet; diese sog. Lageparameter charakterisieren das Ergebnis einer statistischen Reihe. Vorwiegend berechnet man zwei Maßzahlen: das arithmetische Mittel × und die Standardabweichung s. Wir nehmen an, dass der Mitarbeiter im vorliegenden Fall eine durchschnittliche Dichte der Koksbrocken von 1,41 g/cm3 und eine Standardabweichung von 0,02 g/cm3 (gerundet) ermittelt.
Schritt: Schluss von der Stichprobe auf die Grundgesamtheit
Hier klicken zum AusklappenBeispiel
Der Mitarbeiter kann den Schluss ziehen, dass die durchschnittliche Dichte der Koksbrocken in der Grundgesamtheit etwa den Wert 1,41 g/cm3 hat; er kann weiterhin schließen, dass die tatsächliche (unbekannte) Dichte der Grundgesamtheit mit rund 99 %iger Wahrscheinlichkeit im Intervall
$$[-3s+\bar{x};\bar{x}+3s]$$
$$= [-\; 3 \cdot 0,02 + 1,41;\; 1,41 + 3 \cdot 0,02]$$
$$= [1,35;\; 1,47]$$
liegt. Dieser Schluss ist möglich aufgrund der Aussagen, die aus der Normalverteilung abgeleitet werden können.
Es stellt sich weiterhin die Frage, ob das Ergebnis noch weiter verbessert werden könnte, ob also der Mitarbeiter durch eine weitere Stichprobe zu einem Intervall gelangen könnte, in dem die Werte näher beieinander liegen. Die Antwort lautet ja! Der Mitarbeiter könnte den Stichprobenumfang vergrößern (statt z. B. 10 Messwerte werden 30 ermittelt und die durchschnittliche Dichte $$\bar{x}$$ und die Standardabweichung s ermittelt). Es lässt sich mathematisch zeigen, dass mit größerem Stichprobenumfang die Genauigkeit der Schlüsse ansteigt. Gleichzeitig steigen damit aber auch der Zeitaufwand und die Kosten der Untersuchung. Genau diese Frage (Stichprobenumfang, Zeitaufwand, Kosten, statistische Genauigkeit) ist im 2. Schritt (vgl. vorstehend) zu klären. Man wird versuchen, bei gegebenem Aufwand an Zeit und Kosten den Informationsgehalt der Untersuchung zu maximieren. Festzuhalten bleibt aber: einen vollkommen sicheren Schluss von einer Stichprobe auf die Grundgesamtheit gibt es nicht.
Abschließend hat der Mitarbeiter zu entscheiden, ob das Ergebnis seiner Stichprobe die Entscheidung zulässt, den angelieferten Koks anzunehmen oder abzulehnen. Im vorliegenden Fall hängt dies davon ab, ob der Sollwert der Dichte (festgelegt oder mit dem Lieferanten vereinbart) innerhalb des Intervalls liegt oder nicht.
06. Wie erfolgt die Erfassung und Verarbeitung technischer Messwerte?
Die Erfassung und Verarbeitung technischer Messwerte kann unterschiedlich komplex sein; folgende Arbeitsweisen werden unterschieden:
Die Erfassung der Daten erfolgt über eine einfache Messeinrichtung (z. B. Thermometer, Druckmesser); die Prozesssteuerung bzw. ggf. notwendige Eingriffe in den Prozess erfolgen manuell.
Hier klicken zum AusklappenBeispiel
An einer Anlage wird die Temperatur mithilfe eines Thermometers gemessen; wird ein bestimmter Temperaturgrenzwert überschritten, erfolgt eine manuell eingeleitete Kühlung der Anlage durch den Mitarbeiter.
Die Messwerte werden durch die Messeinrichtung erfasst, innerhalb der Messeinrichtung verarbeitet und der Prozess wird automatisch gesteuert (z. B. über Prozessrechner).
Hier klicken zum AusklappenBeispiel
An der Anlage (vgl. oben) wird die Temperatur laufend von einem Prozessrechner erfasst. Bei Erreichen des Grenzwertes erfolgt ein Warnsignal und die Kühlung der Anlage wird ausgelöst.
Elementare Messwertverarbeitung:
Die Verarbeitung der Messwerte erfolgt auf der Basis einfacher mathematischer Operationen (z. B. Summen-/Differenzenbildung in Verbindung mit elektrischer oder pneumatischer Analogtechnik).
Höhere Messwertverarbeitung:
Die Verarbeitung der Messwerte erfolgt auf der Basis komplexer mathematischer Operationen (z. B. Integral-/Differenzialrechnung in Verbindung mit Digitalrechnern).
Hinsichtlich der Form der Datenverdichtung wird weiterhin unterschieden:
Signalanalyse:
Es wird der Verlauf von Messsignalen untersucht (z. B. Verlauf von Schwingungen).
Messdatenverarbeitung:
Aufbereitung, Verknüpfung, Prüfung und Verdichtung von Messdaten.
07. Lassen sich Fehler bei der Erfassung von Messwerten vermeiden?
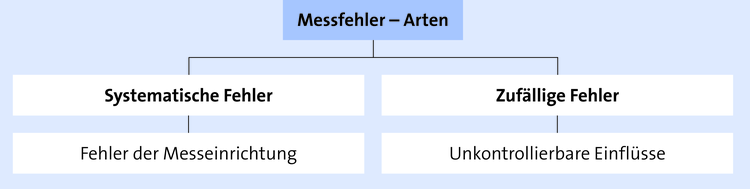
In der Praxis ist jede Messung von Daten (vgl. oben das Beispiel „Dichte der Koksbrocken“) mit Fehlern behaftet. Man unterscheidet zwischen systematischen und zufälligen Fehlern:
Systematische Fehler sind Fehler in der Messeinrichtung, die sich gleichmäßig auf alle Messungen auswirken. Sie lassen sich durch eine verbesserte Messtechnik beheben.
Hier klicken zum AusklappenBeispiel
fehlerhafter Messstab, nicht ausreichende Justierung einer Waage usw.
Zufällige Fehler entstehen durch unkontrollierbare Einflüsse während der Messung; sie sind bei jeder Messung verschieden und unvermeidbar.
Hier klicken zum AusklappenBeispiel
Bei der Untersuchung von Wellen in der Eingangskontrolle stellt man fest, dass von 50 Stück drei fehlerhaft sind; die Wiederholung der Stichprobe kommt zu einem anderen Ergebnis, obwohl die Messverfahren gesichert sind und die Versuchsdurchführung nicht geändert wurde.
Weitere interessante Inhalte zum Thema
-
Personalcontrolling
Vielleicht ist für Sie auch das Thema Personalcontrolling (Durchführen von Personalmaßnahmen) aus unserem Online-Kurs Führen und entwickeln von Personal interessant.
-
Ordinalskala
Vielleicht ist für Sie auch das Thema Ordinalskala (Grundbegriffe der deskriptiven Statistik) aus unserem Online-Kurs Deskriptive Statistik interessant.