Wahrscheinlichkeitsrechnung Online lernen

Dein Vollzugriff auf wiwiweb.de

Mache wiwiweb.de zu deinem Begleiter in deinem Studium oder deiner Aus- und Weiterbildung.

 Vollzugriff auf alle Online-Kurse

sowie alle zukünftigen Erweiterungen und laufende Aktualisierungen

 Alle Lernmaterialien komplett

mit mehr als 480 Videos, 3800 interaktiven Übungsaufgaben und 1750 Lerntexten

 Günstiger als bei Einzelbuchung

nur 14,90 € monatlich bei 12 Monaten Mindestvertragslaufzeit


JETZT BUCHEN für  14,90 €  monatlich

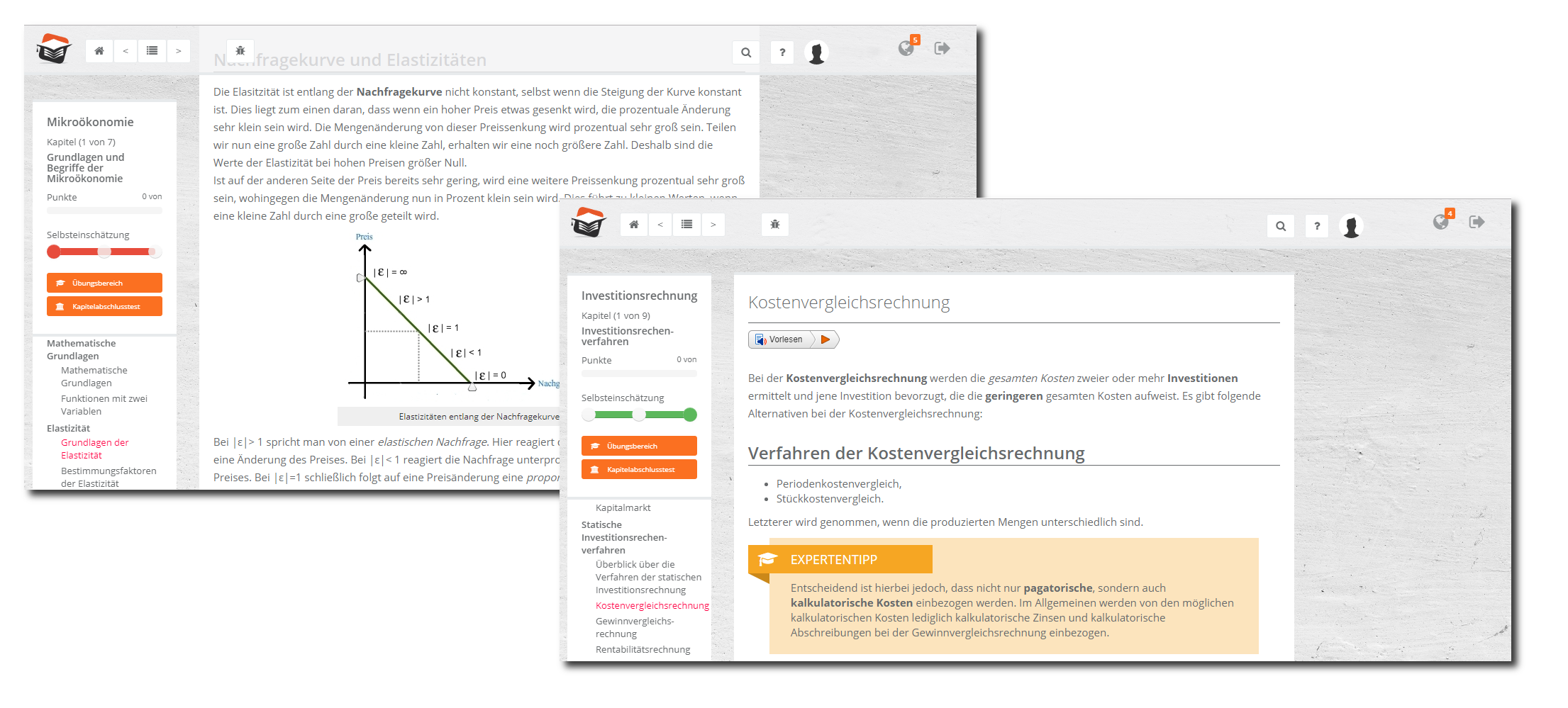
Zunächst behandeln wir die Kombinatorik (Permutationen, Variationen und Kombinationen). Hier ist insb. das Verständnis von Urnenexperimenten wichtig, auch und gerade bzgl. der Unterscheidungen bzgl. Ziehen mit und ohne Zurücklegen und Ziehen mit und ohne Beachten der Reihenfolge.

Alsdann führen wir Wahrscheinlichkeiten ein, und zwar zunächst den Wahrscheinlichkeitsbegriff (nach Laplace, nach Kolmogoroff nach von Mises) und kümmern uns um wichtige Formeln wie den Additionssatz. Eine große Rolle spielen danach bedingte Wahrscheinlichkeiten, die oft in Klausuren mithilfe der Vierfeldertafel, aber auch der Bayesschen Formel inkl. des Satzes von der totalen Wahrscheinlichkeit gelöst werden können.

Danach kümmern wir uns um diskrete und stetige Zufallsvariablen, konkret um Wahrscheinlichkeits- und Dichtefunktionen sowie um die Herleitung der Verteilungsfunktion. Wichtig sind insb. die Binomialverteilung, die geometrische und die Hypergeometrische Verteilung, Poissonverteilung als auch die Exponential- und die Normalverteilung. Breiten Raum nimmt danach die Berechnung von Erwartungswert, Varianz und Standardabweichung ein. Warscheinlichkeiten können nicht nur exakt berechnet, sondern auch angenähert werden. Hierfür sind Approximationsbedingungen wie auch der Zentrale Grenzwertsatz wichtig.

Schließlich findet die Tschebyscheffsche Ungleichung Erwähnung, denn mit ihrer Hilfe können Warscheinlichkeiten zumindest abgeschätzt werden, obwohl die Verteilung der zugrundeliegenden Zufallsvariable, mit Ausnahme von Erwartungswert und Varianz, unbekannt ist.

Die Laufzeit dieses Produktes beträgt 2 Jahre. Das exakte Ablaufdatum wird Ihnen im Warenkorb angezeigt.

Vorteile im Überblick

  • Über 40 Dokumente und mehr als 160 Übungen vermitteln Ihnen umfassend alles Wissenswerte.
    Im Kurs sind darüber hinaus 10 Videos enthalten, in denen die wichtigsten Themen anschaulich zusammengefasst werden. Insgesamt knapp 1.5 Stunden Videomaterial steigern Ihren Lernerfolg und sorgen nebenbei für Abwechslung.
  • Schon mehrere tausend Kursteilnehmer haben sich für unsere Online-Kurse entschieden. Wir haben über viele Jahre Erfahrungen gesammelt und unsere Kursoberfläche stetig verbessert.
  • Das Internet bietet Ihnen weitreichende Möglichkeiten: Lernen, wann und wo Sie möchten. Und daneben gibt es bei uns zahlreiche Features, die zum schnelleren und besseren Lernerfolg beitragen.

Diese Themen werden behandelt

Bitte auf Kapitelüberschriften klicken, um Unterthemen anzuzeigen

Wahrscheinlichkeitsrechnung

Wahrscheinlichkeitsrechnung

  • Kombinatorik

  • Ereignisse

  • Wahrscheinlichkeiten

  • Bedingte Wahrscheinlichkeiten

  • Eindimensionale Verteilungen (ohne Namen)

  • Eindimensionale Verteilungen (mit Namen)

  • Mehrdimensionale Verteilungen

  • Gesetz der großen Zahlen

  • Tschebyscheffsche Ungleichung
Zur Kasse
Wahrscheinlichkeitsrechnung

49,00 €

einmalig
  • 40 ausführliche Lerntexte
  • 10 verständliche Videos
  • 164 Aufgaben zum Üben
  • 40 prägnante Schaubilder
Zur Kasse

Unsere Online-Kurse basieren auf einem erprobten Lernkonzept,
welches erfahrene Dozenten für dich entwickelt haben

Lernvideos
Lerntexte
Übungsaufgaben
Webinaren

Leicht verständliche Lernvideos

Profitieren Sie von einem umfassenden didaktischen Konzept! Sichern Sie sich das kompakte Wissen in den Online-Kursen mit Grundlagentexten, Lernvideos und tausenden interaktiven Übungen. Unsere Dozenten erklären Ihnen in hunderten Lernvideos die schwierigsten Themen leicht verständlich & kompakt.

  • Vertiefung der schwierigsten Themen in hunderten Lernvideos
  • anschauliche Erklärungen
  • perfekte Ergänzung zu den Lerntexten

Diese Inhalte könnten dich auch interessieren


Buchführung

Kursempfehlung

Vielleicht ist es für Sie interessant, dass wir auch einen Kurs zum Thema Buchführung anbieten.